浅谈如何提高初中生的数形结合能力

来源 I 上海市月浦实验学校

 

月浦实验学校　　姚玮

一、           研究背景

在上海市进行的50所初中的学生对各学科的兴趣调查之中，对数学感兴趣的学生仅为13.7%，远低于语文43.2%和英语的29.3%，而在这仅有的对数学表示有兴趣，较为喜欢的学生之中，女学生仅为17.8%，由此可见，学生普遍对数学的兴趣不高，尤其是女学生。而在调查采访中发现，学生认为数学学习中的最大难点就是数形结合的题目，例如函数与几何的结合题目，更有超过60%的学生认为自己的数形结合能力不高，主要表现在图形的空间想象、图形绘制、数与形结合利用的能力不强上。

初中阶段的学生，尤其是女学生，一旦数学成绩不理想，就会产生反感心理，出现不喜欢数学——不愿意主动练习——成绩更不理想——更加反感的恶性循环，而学生往往将这种情况归罪于自身的能力之上，比如产生“我天生不适合学数学”“我的逻辑思维就是不行”这种负面思想，而不认为是自己的学习方法有问题。

二、           数形结合在初中数学教学中的作用

数形结合的能力提升在初中数学教学之中有着重要作用，主要表现在以下几个方面：

1.有助于学生连贯地掌握数学知识点

在整个数学内容之中，数与形都始终形影不离，许多知识点自身就包含数与形的联系性，例如在函数之中，求函数>0的定义域自身就是对不等式的考察，因此学生建立数形结合的能力，能够帮助其将所学的知识点连贯掌握，培养多种解题思路。

2.有效提升数学成绩

无论从研究中还是实际的教学经验中均可见，锻炼学生良好的数形结合能力能够有效提升的解题技巧，通过数形结合的训练，能够给学生更加正确的直觉能力，例如在几何题目之中，题目给出的条件的基础之上，应当如何添线，怎样解题，通过提升这种能力，可以为学生节约大量的生硬计算时间，提升解题技巧，最终提升数学成绩。而在上海市的中考制度之中，数学的中考分数比重为 1/4，提升数学成绩无异于让学生在中考竞争中具有更加大的优势。

3.提升学生发散思维及创造力

我国的学生普遍被指缺乏发散思维和想象力，创造力在世界大国中，也位列倒数，而这样的结果显然不是我们教育者所乐见的。而数形结合的内在含义简言之就是“见到数量就应想到他的几何意义，见到图形就应想到它的数量关系”。 在数学教学之中，通过数与形的转化与结合，能够有效启发学生思路，令其理解题意、分析思考、主动判断反馈，通过培养学生数形结合的能力，不仅能够有效提升学生的空间想象力，更能够为学生提供多样的解题思路及题目条件的联系方法，能够有效提升学生的发散思维。

三、           初中阶段学生学习特点

初中阶段的学生具有这个阶段的特殊性，而掌握学生的心理特点有助于对症下药，提升数学教学水平，总体来说，这个阶段的学生具有以下特点：

1.记忆力尚未开始衰退

初中阶段的学生是学习的黄金时期，在教育心理学之中，初中阶段是学生的记忆力旺盛阶段的尾期（心理学认为，人一生中记忆力最好的时期是3-12岁，这个时期的记忆水平超过遗忘水平，12-16岁记忆和遗忘速度基本持平，需要进行重复记忆从而使短期记忆转为长期记忆，16岁以后记忆力的衰退速度开始逐步超过记忆水平）。因此在这个阶段，应当对学生的良好记忆力加以积极利用。

2.是学生学习习惯和学习兴趣的定型时期

虽说一个人的兴趣是从幼年时开始的，但是在教育心理学之中，幼年及儿童期的兴趣指向仅仅为自我指向，即自己喜欢什么，就对什么产生兴趣，而在青少年期，12-16岁，兴趣的外来指向则发挥出重要的作用。外来指向指的是外在的肯定、褒贬及潜移默化的影响对青少年兴趣的影响性，例如这个时期青少年若听到许多医生的利好消息，则可能会对医学产生兴趣，而在班级之中，若学生的语文成绩始终名列前茅，即使学生对语文并不感兴趣，也会不自觉地倾注兴趣以维持这种优秀成绩。因此这个时期的学习兴趣将会影响到学生终身，不仅影响到学生的进一步教育，也将影响到其未来的研究、择业方向。

四、           提升初中学生数形结合能力的方法

在教学之中，我们教师应当针对学生的特点、学习中的优势及不足进行对症下药，从而实现因材施教的效果。在结合初中生的特点之后，教师可采取的提升学生数形结合的方式有以下几点：

 

1.利用多媒体技术，加大课堂中的图形教学

在传统的教学之中，对于数学图形的绘制主要采用的是黑板手绘，而这样做的缺点就是费时费力，在有限的课时内，能够进行完整绘图、透彻讲解数形变化的机会并不多。而多媒体辅助技术能够有效提升课堂内容容量和图形的绘制视觉感。在当今的多媒体教辅之中，利用几何画板等软件能够快速、准确、有步骤地展现出图像的性质，在多媒体环境下，教师也可以将数与形之间的转换更加明确的展现，有效提升学生对数形结合的直观感受与变化过程的理解，加强数形结合的能力。

2.加大对数形结合的题目的讲解及联系强度和频率

在教学之中，教师应当加大对数形结合题目的讲解和联系频率，如数轴、直角坐标系这种数形结合的典型题目，可有效锻炼学生的数形结合概念和能力。如例题1：点A表示的是-2，点B表示5，若将点A向左移动4个单位长度至C，点B向右移动2个单位长度至D，则点AB之间的距离是多少？若将D再向上平移2个单位长度至E，则△CDE的面积是多少？在这样的题目之中，教师就可通过直观的直角坐标系（如图1-1）表现，让学生直观地看到题目的点A、B的数字范围和移动过程。在教学之中，教师应当加强这样题目的图像绘制和讲解，并鼓励学生自主绘图，提升其对图形的直接想象能力。

 

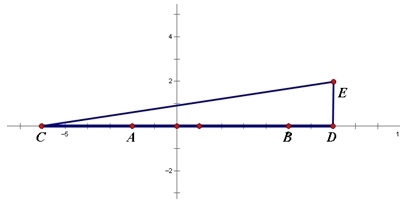
(图1-1：例题1的参考图)

3.在几何题目中，鼓励学生多种思路解题

在教学之中，几何题目是数形结合最典型的题目，也是学生数形结合能力最直接的检验。在教学之中，教师应当鼓励学生多利用发散思维，例如在同一个题目之中，应当鼓励学生利用多种添线方式，进行不同的方法解题，并进行解题难易度的比较。通过这样的训练，能够让学生具有对题目的“直觉”，在面对题目时，具有数形结合的基本思维和能力，在最短时间内寻找到最简洁的解题方式。

 

- THE END-